こんにちは、まさかめです。
今回は数理最適化について解説していきます。
数理最適化とは
数理最適化とは「限られた条件の中で最も効果的な選択肢を求める」ことです。
- 限られた時間の中でどの順番で観光地を巡ると満足度が高くなるのか
- 限られた経費を何に使用すれば利益が大きくなるのか
上記のように何らかの制約条件のもとで、どうすれば目的の値を最大化(最小化)させることができるのかを考えていきます。
ビジネスにおいてよく見られる用途としては以下のようなものがあります。
- 最適解を見つける
▶勤務シフトをどう組むと滞りが発生しないか - 判断を自動化する
▶降水確率に対して傘を持っていくかどうか - 見積り、シミュレーションを行う
▶予算の中で売上を最大化させる商品の組み合わせはどれか
最適化問題の例
最適化問題は様々なものがありますが、よく取り扱われる線形計画問題について説明します。
線形計画問題とは?
1次関数の最大化(最小化)を目的とし、条件がいずれも一次式の最適化問題です。
有名な例として、ナップサック問題などがあります。
題材
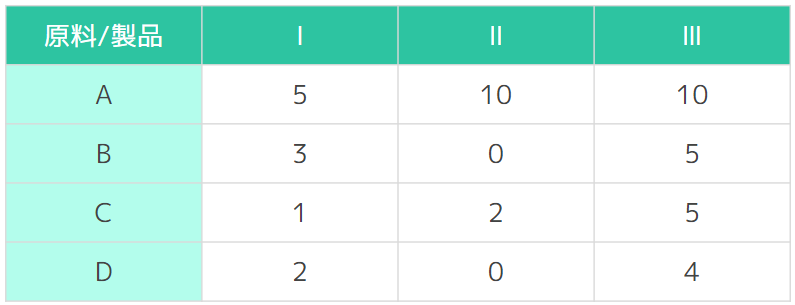
ある工場では4種類の原料A, B, C, Dを用いて、3種類の製品Ⅰ, Ⅱ, Ⅲを生産する(生産量は実数値と仮定)。
以下に示す条件において、利益を最大にするにはⅠ,Ⅱ, Ⅲをどれだけ生産すればよいか、またその時の利益はいくらになるか。
ただし、材料と製品、利益の関係は以下の表に従う。
▼各製品を1単位生産したときの利益(単位:万円)

▼各原料の使用可能量

▼各製品を1単位生産するのに必要な原料の量
定式化
各製品Ⅰ, Ⅱ, Ⅲの生産量をx1, x2, x3とおきます。
その時、総利益は40×1 + 20×2 + 70×3(万円)となり、これを最大化させることが目的です。
また、条件は以下2つとなります。
- 原料の利用可能量をこえてはならない
原料A:5×1 + 10×2 + 10×3 ≦ 90
原料B:3×1 + 5×3 ≦ 30
原料C:1×1 + 2×2 + 5×3 ≦ 50
原料D:2×1 + 4×3 ≦ 10 - 生産量は0以上の整数:x1≧0, x2≧0, x3≧0,
Pythonで解く
Pythonには線形計画問題を解くためのライブラリである「PuLP」というものがあるので、そちらを使用します。
インストールは以下です。
pip install pulp
また、実装は以下となります。
import pulp
problem = pulp.LpProblem(sense=pulp.LpMaximize)
# 変数の定義
# 変数が整数の場合はLpIntegerを指定(デフォルトは連続値)
x1 = pulp.LpVariable('x1', lowBound = 0, cat = pulp.LpInteger)
x2 = pulp.LpVariable('x2', lowBound = 0, cat = pulp.LpInteger)
x3 = pulp.LpVariable('x3', lowBound = 0, cat = pulp.LpInteger)
# 目的関数の設定
problem += 40*x1 + 20*x2 + 70*x3
# 制約条件の追加
problem += 5*x1 + 10*x2 +10*x3 <= 90
problem += 3*x1 + 5*x3 <= 30
problem += 1*x1 + 2*x2 +5*x3 <= 50
problem += 2*x1 + 4*x3 <= 10
# 設定の中身確認
print(problem)
# 実行
status = problem.solve()
print("Status", pulp.LpStatus[status])
# 結果の表示
print("x1 : ", x1.value())
print("x2 : ", x2.value())
print("x3 : ", x3.value())
print("result : ", problem.objective.value())
実行結果は以下となります。

まとめ
今回は数理最適化とは何かを説明し、Pythonで例題を説いてみる実装を紹介しました。
言葉としては馴染みのない数理最適化かもしれませんが、私達の生活で非常に役立っているものなので、ぜひ理解してみてください。